1 Introduction

Machine learning is gaining an ever-growing importance in our lives. As the field is developing, so too are its applications. The traditional machine learning paradigm consists of conceiving a machine learning model, collecting and storing some training data in a central location, then training the model on this data. While this process can be distributed among many processing units, it is still conducted by a single economic entity. This process is appropriate in many settings where quality data is available in large quantities such as image classification, process optimization, or business applications. In other applications, such data is scattered across external devices, each holding a small local dataset that could be used for training. Data generated by mobile applications, or sensitive data such as health data are such examples. In these cases, the high value of the data prevents the model owner from collecting it in a central location.

Federated learning (McMahan et al. 2016) is a new machine-learning paradigm where the model owner and the data owner(s) (also referred to as clients or workers) are separate economic entities. Rather than sharing data between parties, training works as such: the model owner \(MO\) initiates his model. Eligible clients (defined as connected to a power source and a reliable network connection) declare themselves to \(MO\) as being available for training. \(MO\) then randomly selects a subset of those workers and sends them the model. Each client then trains the model on his own local dataset and sends back the gradient updates to \(MO\). Once all updates are received, \(MO\) computes the average update weighted by the number of training samples used by each client, then updates his model. This process is repeated as long as \(MO\) needs to improve his model. This process works under certain conditions.

1. \(MO\) and each client must have an established way of connecting to each other.

2. \(MO\) can either trust or validate the quality of each client’s data. In other words, he is confident that the data points are independent and identically distributed (i.i.d).

3. Clients must be willing to participate in the training and must trust the aggregation process.

Because of these conditions, the range of federated learning applications today is limited. It is best used by software developers, who control the data generated by their application, and can connect to a central server at will. This allows them to meet conditions 1 and 2. Furthermore, with such applications, participation is generally not explicitly asked of the clients, allowing \(MO\) to bypass condition 3.

In order to generalize federated learning to more domains and data sources, one must devise an approach that meets the three conditions above, without needing to control the generation of clients’ data. In this paper, we propose a framework for orchestrating the training procedure that is transparent and provably honest. This paper is structured as such: Section 2 explores previous work into developing such a method; section 3 introduces our proposal for connecting the parties, exchanging model updates, and rewarding clients; section 4 evaluates our proposal with a training simulation; and section 5 explores future work to be done in this direction.

2 Related Work

Many contributions have been made towards generalizing the federated learning process. We summarize them here.

BlockFL (Kim et al. 2019) is an on-chain aggregation mechanism, where model updates are sent to miners, who then add them to a block and propagate them to the network. Aggregation is done on-chain via the FedAvg algorithm (McMahan et al. 2016) to obtain a new global model. One apparent issue with on-chain aggregation is storage. Neural networks consisting of millions or billions of parameters require storage space in the order of megabytes. With the current average block size at around 20 kilobytes (“Ethereum Average Block Size Chart” n.d.), exchanging models on-chain does not scale well.

(Kurtulmus and Daniel 2018) outlines a solution to training a machine learning model using a predefined dataset. In this paradigm, one data owner submits a dataset along with an evaluation function. Workers use those in a race to produce a high-performance model, with the first accepted worker getting a reward. This allows for a valuation of machine-learning training in a decentralized marketplace. This creates a system similar to Bitcoin’s proof-of-work, where miners with valid blocks may not get rewarded for their work. With machine-learning training usually taking hours or days, rather than Bitcoin blocks taking 10 minutes to generate, the amount of wasted time is increased. Nonetheless, the freedom given to data owners for defining an evaluation function is an idea considered in this paper.

When rewarding nodes for their work, one must ensure that nodes are paid fairly. Indeed, the model training is highly dependent on quality data, so clients need to be incentivized not only to participate, but to participate honestly. Some reward mechanisms have been proposed to judge a client’s honesty. The traditional FedAvg algorithm, which weighs the model updates based on the quantity of training data used by each client, is reliant on the i.i.d assumption, which does not always hold up in decentralized systems, and heavily incentivizes dishonest clients to generate fake data or duplicate it.

One approach is to hold a test dataset, and compare the performance of each local model on this dataset. While this approach gives highly-reliable results, it assumes that \(MO\) is willing to share his private testing dataset, which is against the premise of federated learning.

Another approach is to give each client a reputation score that gets updated with every model that he uploads (Zhao et al. 2019). Clients are then selected and rewarded based on their accumulated reputation. Unfortunately, in a decentralized and pseudonymous world, this approach suffers from a few pitfalls: First, it is prone to the cold-start problem, where clients with no reputation will have difficulty building one, regardless of the quality of their data. Indeed, only clients with multiple, diverse datasets will be able to build any meaningful reputation: most clients, who have high-quality specialized datasets, will have difficulty being selected. Second, building reputation does not mean that all one’s datasets will be of high quality: one can build a reputation for a specific domain, which will give him a high chance of getting selected for any domain, where the quality of his data may not be as high as his reputation indicates. Third, as a client builds a good reputation, the incentive to provide quality data decreases: he can now produce cheap low-quality datasets and get rewarded highly based on his past work. Conversely, a client who builds a bad reputation can simply start anew by generating a new identity.

3 Design

This section outlines our proposals for bringing together model owners and clients, aggregating model updates and paying nodes for their contributions.

The main components of our design are an off-chain aggregation server for storing models, a smart contract for rewarding clients, and client software for running the training.

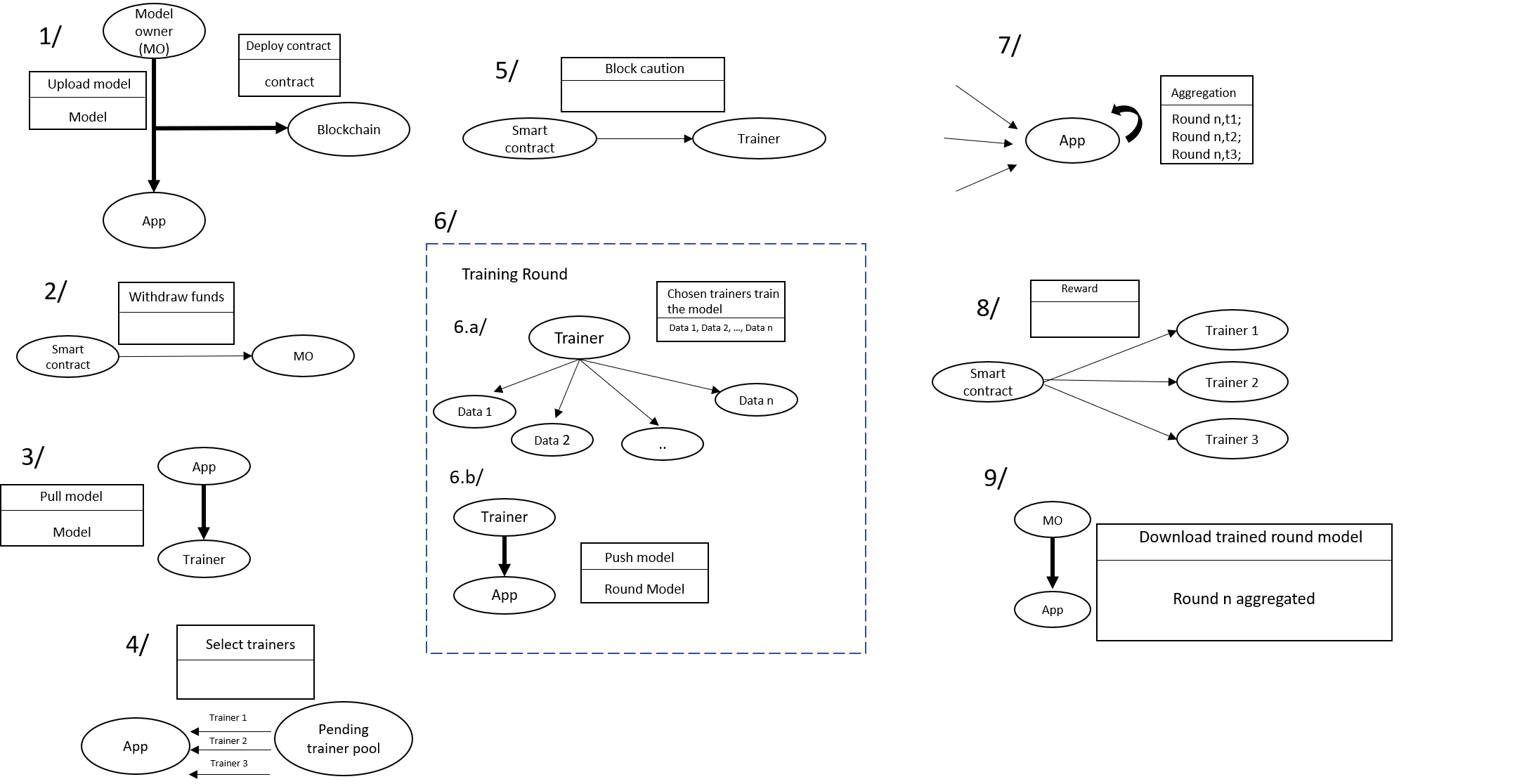
3.1 Connecting the parties

The main purpose of a model owner is finding data to train his model.Therefore, the creation of a stack capable of connecting workers and model owners has been implemented. The model owner is able to upload his model directly through a web interface. When the model’s file is selected, the model owner will be able to configure some parameters for the training such as round’s number, worker’s number required, minimum of workers in the pending pool, type of data required and other basic information such as a short description or the model’s name. Once this piece of information is filled, the model will be available on a marketplace via the web application to all workers. The smart contract will then be triggered to withdraw the fund from the model owner to pay the workers, which corresponds to the total reward that the model owner is willing to give for each round of training. The worker is now able to browse through the catalog and chose a model to train depending on the type of data he has. In order to avoid inappropriate data for the training, the model owner needs to specify a check_data function in his model. This refers to the different criteria that the worker’s data must respect. The model owner must also define a contribution function, which will be used to calculate workers’ rewards. This tells potential workers exactly how much value they can expect their data to generate. Once validation of the chosen model is done, the worker will be added to a pending pool until, the right amount of workers predefined by the model owner, is reached. Validate a model to train also trigger the smart contract that will block a deposit for the worker. This is an approach to limit Sybil attacks, where one replicates his data across several identities. Once reached, the server will then select randomly the right amount of workers from the pending pool then start the training.

3.2 Aggregating model updates

Once a client finishes training, he uploads his update and his contribution to the aggregation server. Upon receipt, the server stores a local copy of the client’s update and stores the worker’s contribution in the smart contract. Once all the clients have finished training, the aggregation server updates the global model using the average of all the client updates, weighted by their contribution scores. As such, FedAvg is the special case where the contribution function equals the number of training points. As the global model is updated, the smart contract starts rewarding the clients.

3.3 Rewarding clients

Each round of training refers to a contribution for the training but also a reward for the workers. These workers will be rewarded at the end of each round. The smart contract created upon, will be triggered and will pay the workers based on the performance and on the amount of reward allocated per round. This amount is calculated as the total of reward given by the model owner divided by the total of rounds.

3.4 Transparency of the process

In this architecture, little trust is needed from the workers to be confident they are rewarded accurately. Indeed, each worker has access to the global model, the contribution function, as well as their local dataset. They can therefore prove the aggregator’s honesty by simply running a round locally on their machine and computing the contribution. This value is exactly what the aggregator stores in the smart contract.

4 Local training loss as a contribution function

We test our approach on the MNIST (LeCun et al. 1998) dataset of digits. We split the training dataset into 20 equal subsets, and assigned each subset to a virtual client. We used a simple two-layer MLP with rectified linear unit pre-activations and a log-softmax output activation, and trained for 15 rounds (we considered one training epoch as one round)

We used the inverse of the local training loss as our contribution function. The rationale is the following: a capable model should be able to find patterns on data that is distributed similarly to what the model has been trained on. Therefore, high-quality data should cause it to generate a low training loss. Additionally, training it on a large amount of data should also help reducing the loss, Training loss therefore simultaneously incentivizes clients to not only train on good data, but also to train on a large quantity of it. Furthermore, as the training loss is needed to train the model regardless of the contribution function, using it to calculate the contribution adds little extra computation. In fact, only an averaging is required, and its computation is linear in the number of training points.

Before every training round, any number of clients could be replaced by malicious clients. We considered a malicious client as performing one of the following three attacks:

1. Sybil attacks (client replicates his data across several identities)

2. Data duplication attacks (client duplicates his data)

3. Poisoning attacks (client uses random noise as training data)

4.1 Results

We compared the test accuracy of our method to that of FedAvg for each attack and for any number of malicious clients from 0 to 19 (i.e. 95% of the data is malicious). Results follow.

4.1.1 Baseline Model Performance

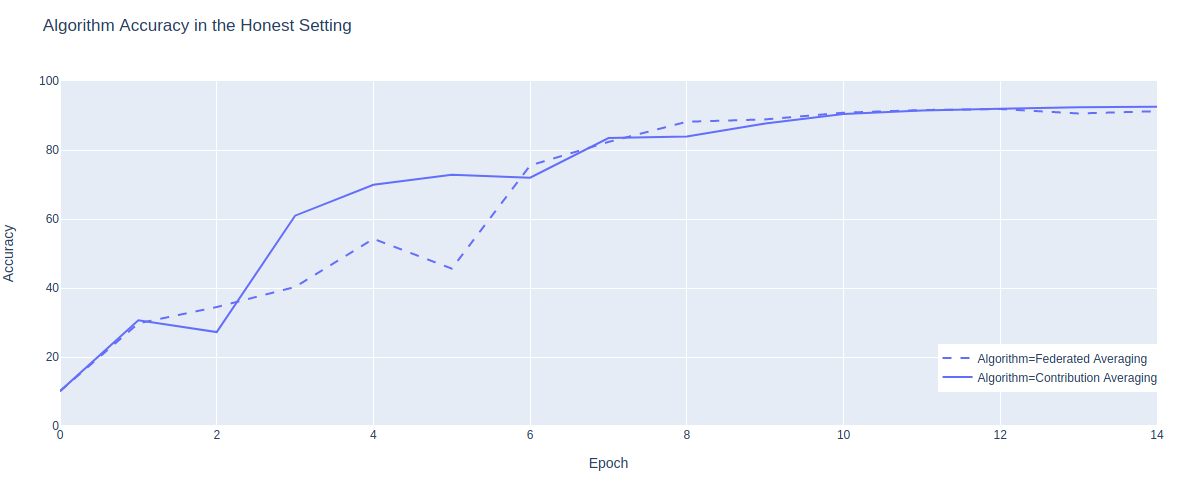
As a baseline check, we compare the model’s performance using both methods, when all clients are honest and provide quality data (Figure 2). Both methods achieve almost identical final scores of over 90%, and have similar learning curves. With the dataset being randomly shuffled and split equally between the clients, the local losses should be fairly similar, which explains the similarity of the learning curves.

4.1.2 Contribution evolution over time

The primary motive for defining a contribution function is to prevent malicious clients from affecting model training and being rewarded as if they were honest. Figure 3 shows the average contribution of malicious clients at every round, for the situation where 15% of the data is controlled by malicious clients, and those clients are present from the first round to the last.

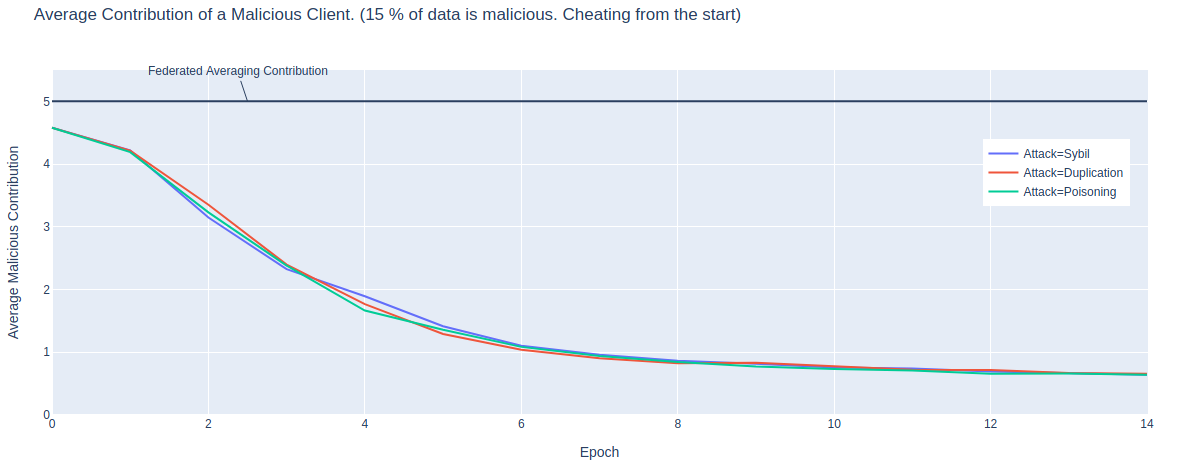
With standard federated averaging, the contribution is defined as the number of training points: in this simulation, FedAvg attributes each client 5% of the total contribution. With local training loss, the contribution of each malicious client drops to less than 1% of the total contribution. Because the loss function used in this simulation (negative log-likelihood) outputs a positive number, malicious clients would always receive some contribution. However, as this number approaches zero, so too does the incentive to cheat.

4.1.3 Performance limit

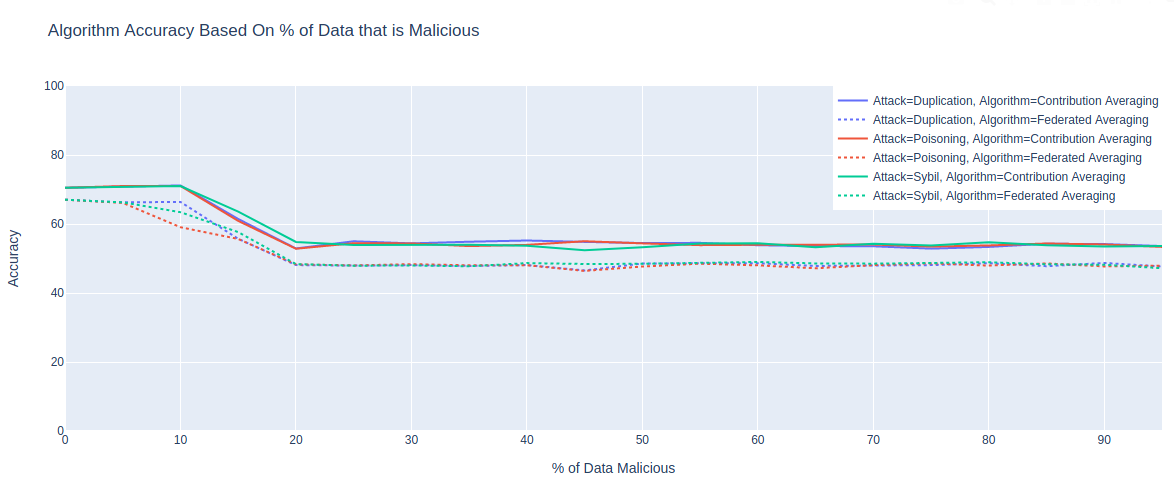
While training loss shows a better ability to detect and adjust against malicious data, this ability is dependent on the proportion of data being malicious. As shown in Figure 4, both methods lost significant capability when dealing with 20% or more malicious data. This could be remedied in a few ways. First, the model can be pre-trained by \(MO\) using his local dataset. Second, \(MO\) can add a penalty term either in the contribution function to reduce a client’s contribution, or in the data checking function to reject it entirely. This term can be based e.g. on a similarity measure between the client’s distribution and an expected distribution.

5 Limitations and Future Work

This section outlines areas of improvement to be considered.

5.1 Centralized aggregator

The high cost of storing models and averaging updates requires these operations to be done off-chain. Our framework makes use of a third-party secure aggregation server to perform this task. While the server is provably honest to the clients, \(MO\) has to trust that the clients were truly selected randomly and that the model updates were done in accordance to the calculated contributions. Using decentralized storage such as IPFS (Benet 2014) would help mitigate that issue and would give \(MO\) full control over model updates. However, the open storage of machine learning models can be a privacy issue, and a third-party will still be required for the random selection of clients.

The clients could be selected randomly by making them solve a puzzle and send in a proof of work similar to how Bitcoin miners are selected: in this case, the first \(N\) clients to complete the proof of work would be automatically selected to train, where \(N\) is the number of workers specified by \(MO\). This would remove the need for a minimum worker pool, and would allow for randomness without a third-party. The minimum deposit requirement would be replaced by a difficulty parameter, similar to the ones adjusted by current blockchains. However, true randomness would only be achieved if all clients had the same processing power. As this is unlikely to be the case, this proof-of-work mechanism will favor clients with the most computing resources, and not necessarily those with the best data.

5.2 Predetermined per-round reward

The smart contract automatically calculates the reward per round as the total reward remaining to be paid divided by the number of rounds left. This reward is then spread among the clients according to their share of the total contribution for the round. This ensures that the smart contract has enough funds to allow clients to withdraw their balance at any time. However, this also pays out the same total reward on each round, although the model’s improvement slows down over time. This should be reflected in the total rewards paid. \(MO\) can currently achieve this by withdrawing funds before a round starts, reducing the total reward. This requires him to download the updated global model and calculate its performance, lacking the convenience of an automated method.

6 Conclusion

In this paper, we have outlined a transparent, provably-honest, general-purpose framework for decentralized federated learning. This framework allows parties to connect together and perform training sessions regardless of the domain in which their data lies. It requires little trust from the parties and is highly configurable my the model owner, giving him control over the quality of the data being submitted by clients.